
Season 1
Overview
Nine chapters, two hours of maths, that take you gradually up to the fourth dimension. Mathematical vertigo guaranteed!
Episodes
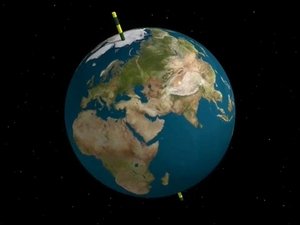
1. Dimension Two
2008-07-18
Hipparchus explains how two numbers can describe the position of a point on a sphere. He then explains stereographic projection: how can one draw a picture of the Earth on a piece of paper?
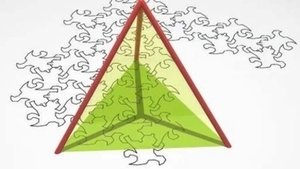
2. Dimension Three
2008-07-25
M. C. Escher tells the adventures of two-dimensional creatures who are trying to imagine three-dimensional objects.
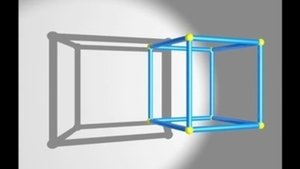
3. The fourth dimension (1)
2008-08-01
Mathematician Ludwig Schläfli talks to us about objects in the fourth dimension and shows us a procession of regular polyhedra in dimension 4, strange objects with 24, 120 and even 600 faces!

4. The fourth dimension (2)
2008-08-08
Mathematician Ludwig Schläfli talks to us about objects in the fourth dimension and shows us a procession of regular polyhedra in dimension 4, strange objects with 24, 120 and even 600 faces!
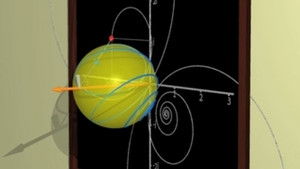
5. Complex Numbers (1)
2008-08-15
Mathematician Adrien Douady explains complex numbers. The square root of negative numbers is explained in simple terms. Transforming the plane, deforming pictures, creating fractal images.

6. Complex Numbers (2)
2008-08-22
Mathematician Adrien Douady explains complex numbers. The square root of negative numbers is explained in simple terms. Transforming the plane, deforming pictures, creating fractal images.
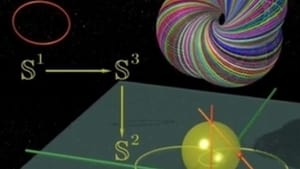
7. Fibration (1)
2008-08-29
The mathematician Heinz Hopf describes his "fibration". Using complex numbers he builds beautiful arrangements of circles in space.

8. Fibration (2)
2008-09-05
The mathematician Heinz Hopf describes his "fibration". Using complex numbers he builds beautiful arrangements of circles in space.

9. Proof
2008-09-12
Mathematician Bernhard Riemann explains the importance of proofs in mathematics. He proves a theorem on stereographic projection.